simhash海量文本去重的工程化
simhash算法是google发明的,专门用于海量文本去重的需求,所以在这里记录一下simhash工程化落地问题。
下面我说的都是工程化落地步骤,不仅仅是理论。
背景
互联网上,一篇文章被抄袭来抄袭去,转载来转载去。
被抄袭的文章一般不改,或者少量改动就发表了,所以判重并不是等于的关系,而是相似判断,这个判别的算法就是simhash。
simhash计算
给定一篇文章内容,利用simhash算法可以计算出一个哈希值(64位整形)。
判别两篇文章是相似的方法,就是两个simhash值的距离<=3,这里距离计算采用汉明距离,也就是2个simhash做一下异或运算,数一下比特位=1的有N位,那么距离就是N。
现在问题就是,如何计算文本的simhash?
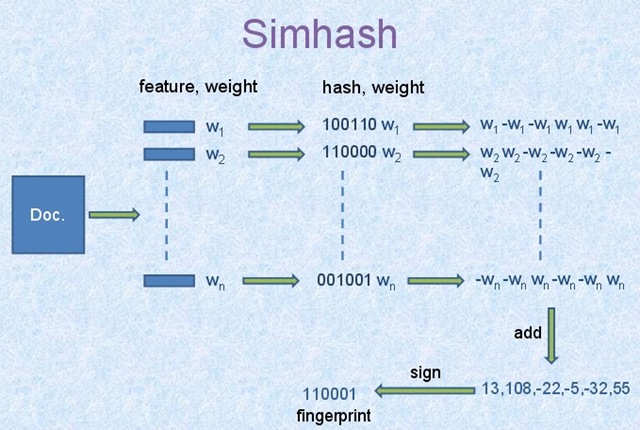
分词+权重
首先需要将文章作分词,得到若干个(词组,权重)。
分词我们知道很多库都可以实现,最常见的就是结巴分词。权重是怎么得来的呢?
权重一般用TF/IDF算法,TF表示词组在本文章内的频次比例,出现越多则对这篇文章来说越重要,文章分词后TF可以立马计算出来。
IDF是词组在所有文章中的出现比例,出现越多说明词组对文章的区分度越低越不重要,但是IDF因为需要基于所有文章统计,所以一般是离线去批量计算出一个IDF字典。
结巴分词支持加载IDF词典并且提供了一个默认的词典,它包含了大量的词组以及基于海量文本统计出来的IDF词频,基本可以拿来即用,除非你想自己去挖掘这样一个字典。如果文章产生的分词在IDF字典里不存在,那么会采用IDF字典的中位数作为默认IDF,所谓中庸之道。
所以呢,我建议用结巴分词做一个分词服务,产生文章的(分词,权重),作为simhash计算的输入。
TOP N词组参与计算
文章分词产生的词组太多,一般我们取TF/IDF最大的N个,这个N大家看心情定。
对于每个词组,套用一个哈希算法(比如times33,murmurhash…)把词组转换成一个64位的整形,对应的二进制就是01010101000…这样的。
接下来,遍历词组哈希值的64比特,若对应位置是0则记为-权重,是1就是+权重,可以得到一个宽度64的向量:[-权重,+权重,-权重,+权重…]。
然后将TOP N词组的向量做加法,得到一个最终的宽64的向量。
生成simhash
接下来,遍历这个宽度64的向量,若对应位置<0则记录为0,>0则记录为1,从而又变成了一个64比特的整形,这个整形就是文章的simhash。
海量simhash查询
抽屉原理
之前说过,判定2篇文章相似的规则,就是2个simhash的汉明距离<=3。
查询的复杂性在于:已有100亿个文章的simhash,给定一个新的simhash,希望判断是否与已有的simhash相似。
我们只能遍历100亿个simhash,分别做异或运算,看看汉明距离是否<=3,这个性能是没法接受的。
优化的方法就是”抽屉原理”,因为2个simhash相似的标准是<=3比特的差异,所以如果我们把64比特的simhash切成4段,每一段16比特,那么不同的3比特最多散落在3段中,至少有1段是完全相同的。
同理,如果我们把simhash切成5段,分别长度 13bit、13bit、13bit、13bit、12bit,因为2个simhash最多有3比特的差异,那么2个simhash至少有2段是完全相同的。
建立索引
对于一个simhash,我们暂时决定将其切成4段,称为a.b.c.d,每一段16比特,分别是:a=0000000000000000,b=0000000011111111,c=1111111100000000,d=111111111111111。
因为抽屉原理的存在,所以我们可以将simhash的每一段作为key,将simhash自身作为value追加索引到key下。
假设用redis做为存储,那么上述simhash在redis里会存成这样:
key:a=0000000000000000 value(set结构):{000000000000000000000000111111111111111100000000111111111111111}
key:b=0000000011111111 value(set结构):
{000000000000000000000000111111111111111100000000111111111111111}
key:c=1111111100000000 value(set结构):
{000000000000000000000000111111111111111100000000111111111111111}
key:d=111111111111111 value(set结构):
{000000000000000000000000111111111111111100000000111111111111111}
也就是一个simhash会按不同的段分别索引4次。
判重
假设有一个新的simhash希望判重,它的simhash值是:
a=0000000000000000,b=000000001111110,c=1111111100000001,d=111111111111110
它和此前索引的simhash在3段中一共有3比特的差异,符合重复的条件。
那么在查询时,我们对上述simhash做4段切割,然后做先后4次查询:
用a=0000000000000000 找到了set集合,遍历集合里的每个simhash做异或运算,发现了汉明距离<=3的重复simhash。
用b=000000001111110 没找到set集合。
用c=1111111100000001 没找到set集合。
用d=d=111111111111110 没找到set集合。
优化效果
经过上述索引与查询方式,其实可以估算出优化后的查询计算量。
假设索引库中有100亿个simhash(也就是2^34个simhash),并且simhash本身是均匀离散的。
一次判重需要遍历4个redis集合,每个集合大概有 2^32 / 2^16个元素,也就是26万个simhash,比遍历100亿次要高效多了。
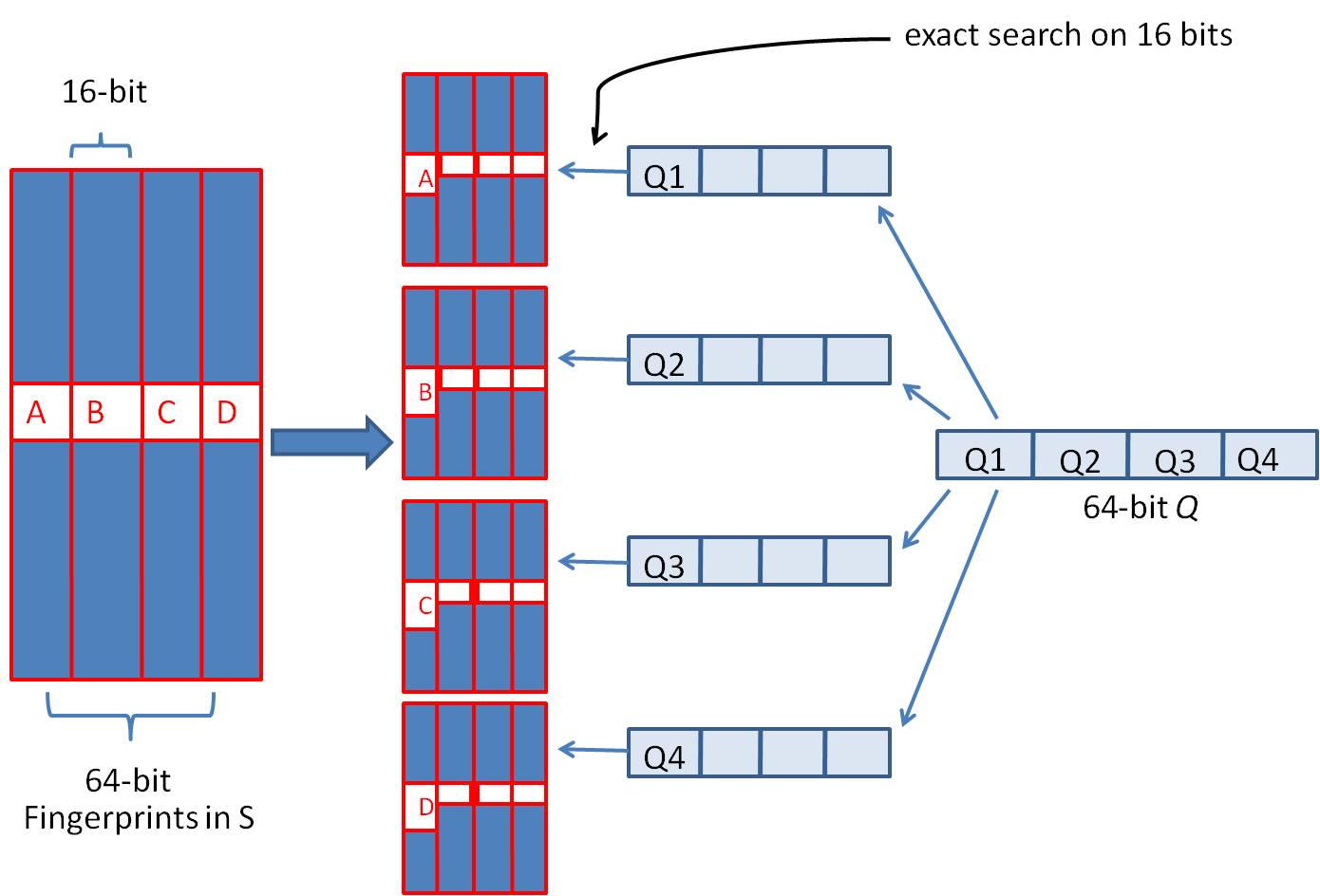
图片左侧表示了一个simhash索引了4份,右侧表示查询时的分段4次查找。
权衡时间与空间
假设分成5段索引,分别命名为:a.b.c.d.e。
根据抽屉原理,至多3比特的差异会导致至少有2段是相同的,所以一共有这些组合需要索引:
- a,b
- a,c
- a,d
- a,e
- b,c
- b,d
- b,e
- c,d
- c,e
- d,e
一个simhash需要索引10份,一个集合的大小是2^34 / 2^(26)=256个。
一次查询需要访问10次集合,每个集合256个元素,一共只需要异或计算2560次,基本上查询性能已不再是瓶颈。
但是也可以知道,因为冗余的索引份数从4份变成了10份,所以其实是在牺牲空间换取时间。
对应的,这么大量的存储空间,再继续使用redis也是不可能的事情,需要换一个依靠廉价磁盘的分布式存储。
存储选型
毫无疑问选择hbase,特别适合SCAN遍历集合。
rowkey设计:4字节的segment+1字节的段标识flag+8字节的simhash。
切4段,索引一段需要16比特;切5段,索引2段需要13+13比特;所以用4字节的segments来存段落。
1字节的抽屉标识,比如是切4段则标识是1,2,3,4;切5段则可以是1,2,3,4,5,6,7,8,9,10,分别代表(a,b),(a,c),(a,d),(a,e),(b,c) …
然后最后追加上simhash自身作为区分值,这样在查询时只需要指定segment+flag做4/10次SCAN操作,进行异或运算即可。
如果文章帮助您解决了工作难题,您可以帮我点击屏幕上的任意广告,或者赞助少量费用来支持我的持续创作,谢谢~

最后一部分,4字节的segments,从哪里来,是什么,可以举个例子吗?这个细节没看懂?
先认真从头读几遍,还是不理解可以加我QQ给你说下:120848369.
4 字节的 segment 是指 切5段时,2段需要13+13比特,26/8 占4个字节吗
对的,抽屉原理。
5段,就得索引其中的2段(13+13bits),26/8 > 3,所以就是用4字节来存相同的部分。
谢谢,关于抽屉和存储这部分,非常赞
客气~
感觉是,用空间换取了异或操作的计算耗时
100w数据 去重的话,需要耗时多少? 我用python写的,数据存在字典里,耗时特别长
与抽屉的规模有关,正确实现不应该存在严重耗时,时间复杂度属于常数。
想问一下,分块有要求么?比如64为的simhash,分成四段16,16,16,16,那可不可以分成28, 12,12,12。后者的分法有什么问题么?
我认为没问题,不违背抽屉原理。
请教一下博主,hashcode比较的时候,如果不分段,放在Elasticsearch里边,Elasticsearch能支持这种百万级的查询匹配吗?
不适合
es的每行doc定义成(hashcode,seg1,seg2,seg3,seg4),每个seg字段开启索引,然后并发4路seg查询scan,这样会有什么问题吗
es的每行doc定义成(hashcode,seg1,seg2,seg3,seg4),每个seg字段开启索引,然后并发4路seg查询scan,这样会有什么问题吗
请教一下博主,hashcode比较的时候,如果不分段,放在Elasticsearch里边,Elasticsearch能支持这种百万级的查询匹配吗?
不适合。
给博主一个Mua
给博主赞助5块钱才是真爱。
海明距离小于三,判断相似要求是不是高了一些
我没实践过,你可以试试。
64bit 下 平均海明距離32 小於等於3的確是高,但在有幾億數據量的情況下應該是還好
64bit 下 平均海明距離32 小於等於3的確是高,但在有幾億數據量的情況下應該是還好
赞! 非常清晰
感谢,请打赏
反向一下,一个长文本如何躲避simhash查重呢?
有什么好想法可以贴上来帮助其他人。
1