numpy机器学习 – L2正则化
本文介绍如何推导L2正则化,涉及到数学推导没法事无巨细,所以下面只是一个大概的流程记录。
理论简述
根据前面几篇博客,我们知道通过引入2次项与更高的项次可以解决线性不可分的数据分布问题,此时分类的边界线呈现出弧线效果。
但是如果我们对输入x向量做太高的次方项的话,模型训练就容易”过于拟合”训练数据,反而对测试集的表现就不好了,这是我们认为模型过于复杂了,如果不能有更大量的训练样本来学习的话,那么就表现为泛化能力差。
遇到”过拟合”的话,可以减少模型的N次项来降低模型复杂度以便让分界线更直一些即可,另外一种思路就是使用”正则化”技术。
以回归问题为例,下面分别是原先的目标函数,我们的目标是不停的调整theta来令函数值尽量小:
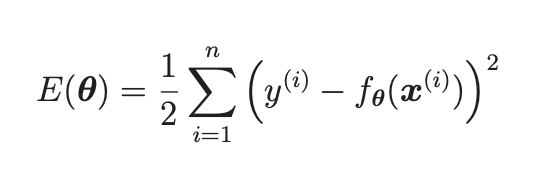
该目标函数里面只会涉及到theta的2次项,所以其函数曲线如下:
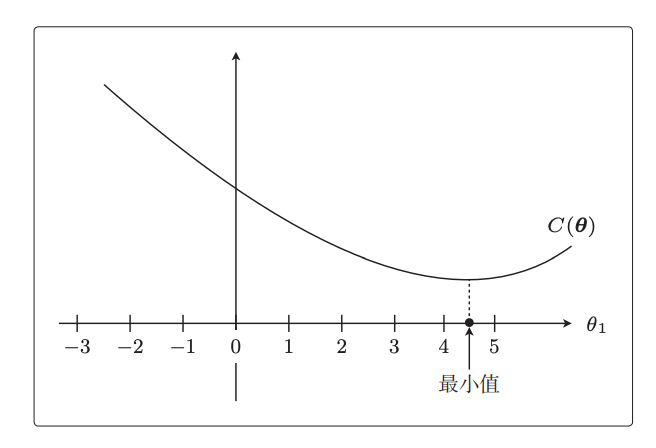
也就是说通过不停的求偏导数修正theta(梯度下降),最终theta会调整到4到5之间,整个目标函数接近了最小值,这就是我们机器学习的核心要义啊。
现在我们定义R为正则项,把它加入到目标函数中:
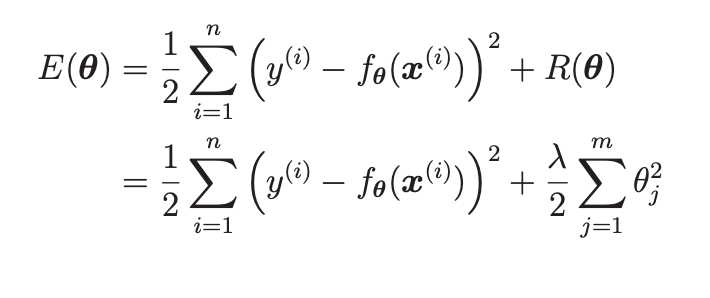
R项也是关于theta的函数,我们把原目标函数与正则项函数的曲线画出来:
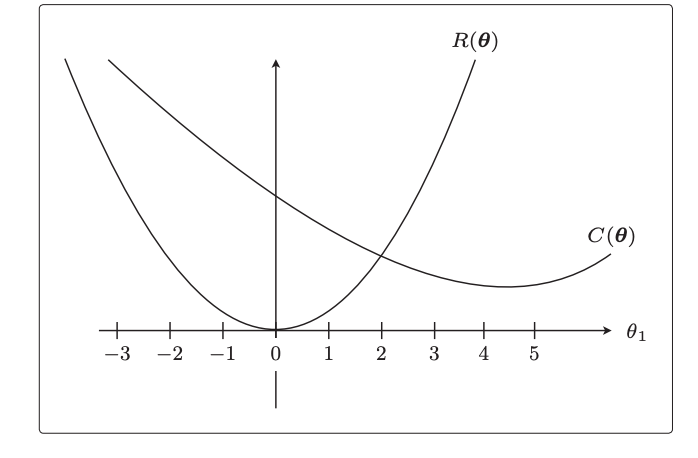
因为新的目标函数是原目标函数+正则项函数,所以我们把2个曲线的高度想加,画出想加后的曲线:
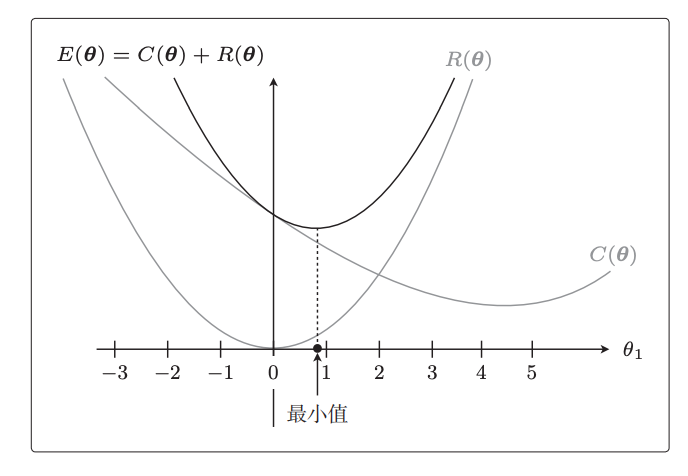
深色的曲线就是新的目标函数,它取最小值时的横坐标(theta)更接近于0,也就是说同样是优化目标函数,加入正则项后这个theta的取值会更小,对于最终学习后的回归函数来说就意味着:
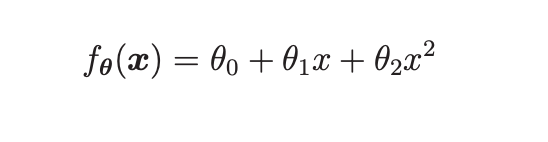
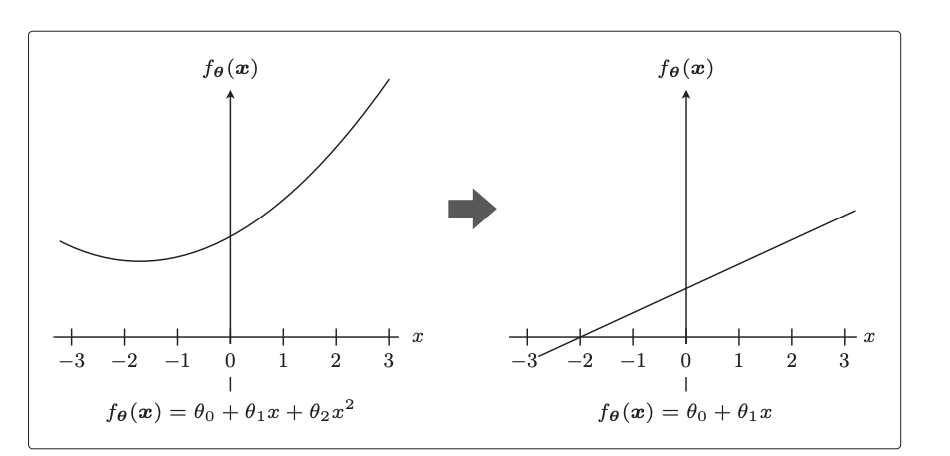
可能x二次方项式前面的theta值几乎为0,这样的话回归函数就相当于被正则化惩罚为了1次项模型,因此曲线不会那么弯曲,也就避免了过拟合。
至于正则化项前面的lambda系数,如果为0就相当于不应用正则化:
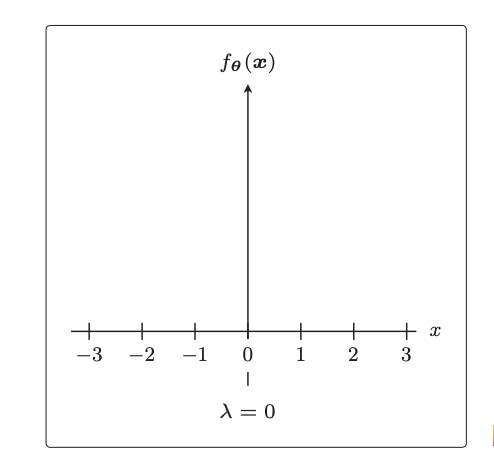
否则lambda越大则正则化的曲线越收拢在y轴,可以把目标函数取最小值时的theta位置也拉向theta=0的位置,也就是会导致theta更小,即更大程度的打压了”过拟合”情况:
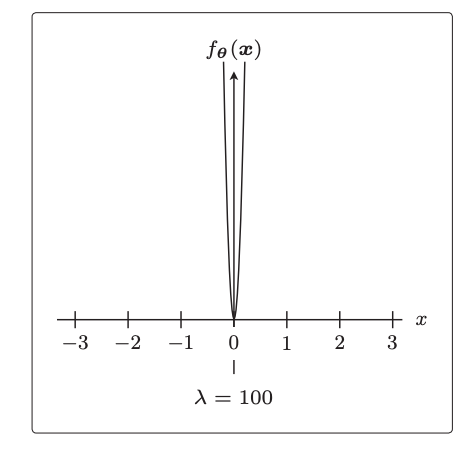
对于逻辑回归分类的目标函数来说,优化目标是概率最大化,所以是”梯度上升”找最大值的位置:
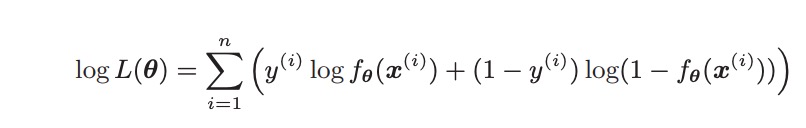
与正则化函数曲线开口向上来拉扯最小值的出现位置是矛盾的,所以只需要取反来把最大化问题转成最小化问题,这样就可以符合上述要求:
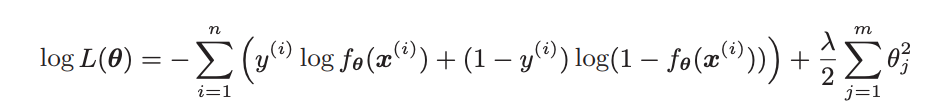
上述第一项就是原先的部分,我们只需要对后面正则化这部分求偏导并加入到微分结果里即可。
代码开发
我们以逻辑回归分类器为例。
数据如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
x1,x2,y 153,432,0 220,262,0 118,214,0 474,384,1 485,411,1 233,430,0 396,321,1 484,349,1 429,259,1 286,220,1 399,433,0 403,300,1 252,34,1 497,372,1 379,416,0 76,163,0 263,112,1 26,193,0 61,473,0 420,253,1 |
加载数据,对x1与x2特征分别做标准化:

我们将回归函数做成包含常数项和x1二次项的样子:
我们引入L2正则的强度系数,越大则会导致theta越小,模型的高次项系数就越接近于0,这样分界线就越直:

训练过程关键是原目标函数前面加了负号,将原先的最大化目标函数转成了最小化问题,然后再加上正则化项的偏导数:
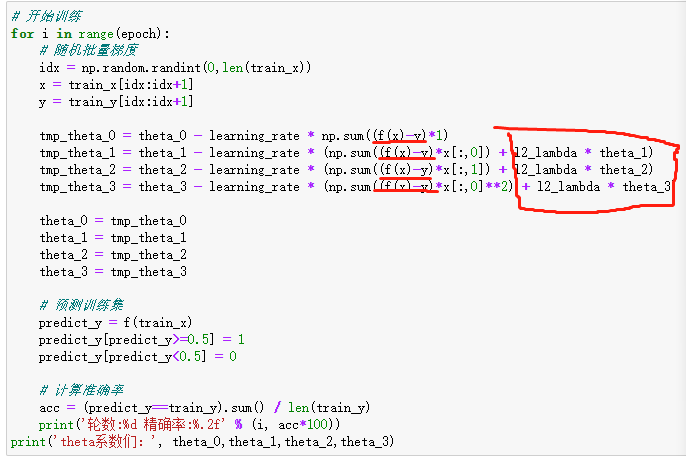
最后发现训练出的模型对训练集准确率不是100%,并不能继续完全拟合到训练集:
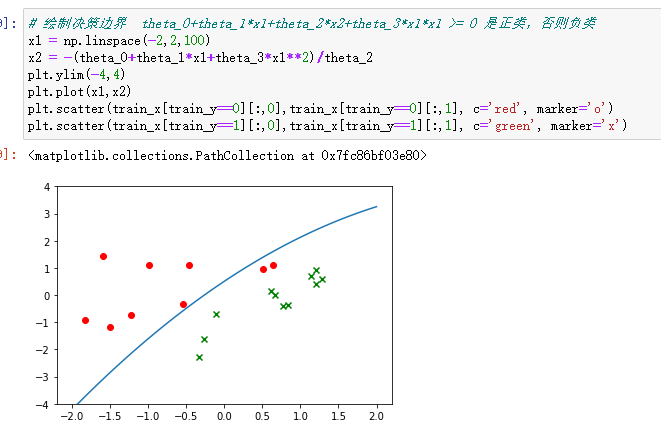
新目标函数引入了>=0的正则项函数,这个优化目标就不如原先纯粹了,theta系数的平方和与损失似乎没有什么关系,所以引入正则项的目标函数就像是干扰训练一样,使得theta不能达到某种最优,从另一方面看就是theta更加贴近于0,从而使得模型变得“简单”,避免了“过拟合”问题。
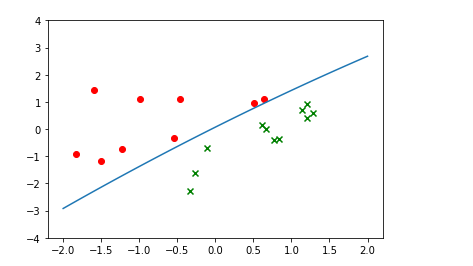
如果我们只对x1的二次项theta引入正则化,其他theta不引入正则化,则x1二次项的theta系数几乎为0,分界线几乎变成了直线:

numpy机器学习系列的源码我放在这里:https://github.com/owenliang/numpy-ml
如果文章帮助您解决了工作难题,您可以帮我点击屏幕上的任意广告,或者赞助少量费用来支持我的持续创作,谢谢~

1