numpy机器学习 – 实现神经网络-下(实现篇)
接前文《numpy机器学习 – 实现神经网络-上(理论篇)》,我们在深刻理解理论之后,实现时只需要避开几个小坑即可。
项目地址:https://github.com/owenliang/MLP
神经网络的构成为:
- 1个输入层
- 1~n个隐层
- 1个输出层
训练流程涉及:
- 前向传播
- 计算输出层误差,反向传播误差
- 计算所有链接权重的梯度,更新链接权重
下面我们按训练流程拆解展示代码,蓝色字体表示容易犯错的地方。
初始化网络
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import numpy as np from scipy.special import expit class NeuralNetwork: """ 初始化函数 input_size: 输入层神经元个数 hidden_layers: 一个列表,每层隐层的神经元个数 output_size:输出层 """ def __init__(self, input_size, hidden_layers, output_size, learning_rate = 0.01, output_activation = False): self.input_size = input_size self.hidden_layers = hidden_layers self.output_size = output_size self.learning_rate = learning_rate self.output_activation = False self.layer_weights = [] # 经验A:初始化权重一定要有正有负,否则训练可能无法收敛 # 输入层到第1个隐藏层 self.layer_weights.append(np.random.random((hidden_layers[0], input_size)) - 0.5) # 隐藏层到隐藏层 for i in range(len(hidden_layers) - 1): self.layer_weights.append(np.random.random((hidden_layers[i+1], hidden_layers[i])) - 0.5) # 最后的隐层到输出层 self.layer_weights.append(np.random.random((output_size, hidden_layers[-1])) - 0.5) |
神经网络的关键就是初始化层与层之间的权重矩阵,包含这些:
- 输入层->第1个隐层
- 隐层->隐层
- 隐层->输出层
使用NeuralNetwork时允许用户这样传参控制网络结构:
|
1 2 |
# 定义神经网络 nn = NeuralNetwork(input_size=1, hidden_layers=[5,4,2], output_size=1, learning_rate=0.001, output_activation=False) |
nn网络的结构为:
- 输入层只有1个神经元
- 有3个隐层,每层神经元个数依次为5个,4个,2个
- 输出层只有1个神经元
nn的学习率是0.001,同时output_activation=False指定输出层神经元不使用激活函数,这意味着nn是用来做回归预测的模型。
因为前向计算是逐层前馈的,我们将上述层与层之间的权重矩阵都放到一个list中,后续的逐层前向计算时就可以利用for循环迭代完成,因此无论用户设置多少个隐层都可以保持通用性。
链接的权重是随机生成的,我们利用random生成0~1之间的随机小数再减去0.5,这样权重的范围就是-0.5~0.5之间,在实践中初始化权重的取值范围非常重要,一开始我直接采用了0~1范围生成权重,发现有一定的几率导致模型失控无法收敛,这里的经验就是初始化权重一定要有正有负。
前向计算
输入层神经元的输出就是原始特征,经过层层向后传播到达输出层,因此训练函数的一开始就是完成这样一个迭代式的前向传播过程:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
""" 训练函数 inputs:训练输入 outputs:训练输出 """ def train(self, inputs, outputs): # 将矩阵转置,用于后续矩阵运算 x = np.array(inputs, dtype=np.float).T y = np.array(outputs, dtype=np.float).T """ 前向计算 """ layer_outputs = [x] for i in range(len(self.layer_weights)): x = np.dot(self.layer_weights[i], x) if i != len(self.layer_weights) - 1 or self.output_activation: # 非输出层 or 输出层应用激活 x = expit(x) layer_outputs.append(x) |
用户输入的训练样本通常是行模式,而神经网络中神经元是纵向排列的关系才能实现矩阵点乘计算,因此我们我们假定要对输入训练样本的x和y做转置。
为了后续计算梯度,我们需要记住每一层神经元的输出,因此layer_outputs用于完成这个工作,输入层的输出就是原始特征x,而后续层的神经元输出则是由前一层神经元输出与链接权重做点乘并经过激活函数sigmoid而产生的。(上面的expit就是sigmoid函数)
这里需要注意,隐层神经元总是需要应用激活函数,但是输出层神经元需要根据模型的任务来决定是否应用激活函数:
- 如果是分类问题,那么输出层也应该使用激活函数,这样输出的就是对应分类的概率。
- 如果是回归问题,那么输出层不应该使用激活函数,否则输出值被压扁到0~1之间,永远不可能拟合训练目标。
上述if语句就是为了判断这个问题而存在的,不需要继续展开解释。
层与层之间的运算如下图所示,我们在上篇博客讲过,在此仅帮助回忆:
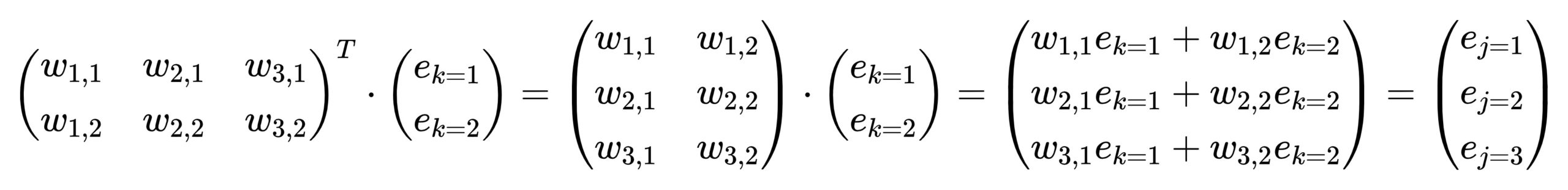
计算输出层误差,反向传播误差
既然前向传播得到了模型的输出,那么就计算一下模型输出和真实目标之间的误差,每个输出层的神经元都有自己的误差,请大家回顾一下该图:
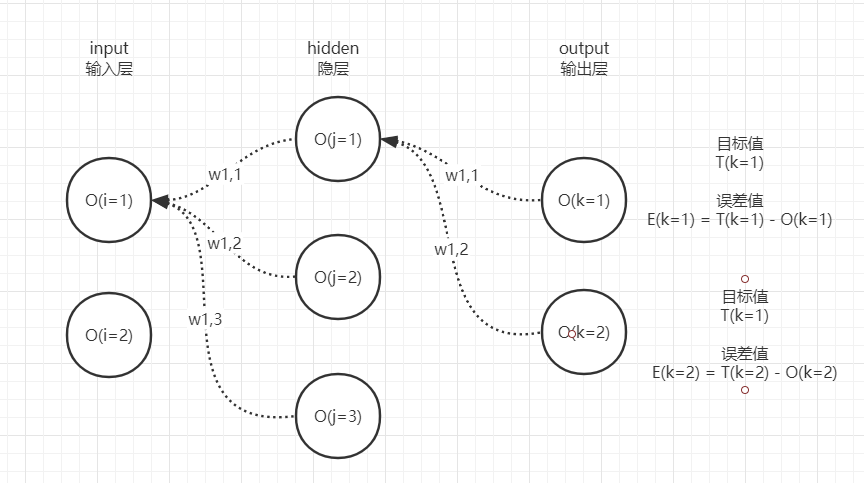
计算出2个神经元的误差后,就需要沿着从右到左的过程反向传播误差到网络左侧的神经元,为后续计算梯度做准备。
|
1 2 3 4 5 6 7 |
""" 反向传播误差 """ layer_errors = [y-layer_outputs[-1]] for i in range(len(self.layer_weights)-1, 0, -1): # 误差只需要传播到第1个隐层即可 layer_errors.append(np.dot(self.layer_weights[i].T, layer_errors[-1])) layer_errors.reverse() |
因为计算梯度需要,我们需要记住每一层神经元输出的误差,将它们记录在layer_errors列表中。
误差从右往左反向迭代计算,因此叫做反向传播,实际与正向传播仅仅是方向和传播的内容不一样而已,因此计算就是逐层完成的。
这里需要注意,输入层不需要计算误差,因为输入层与第1个隐层之间的链接梯度不依赖输入层的误差,因此for循环会提前1次终止。
因为误差是从右往左append到列表中的,我们将它反转一下,方便后续梯度计算的时候方便与layer_outputs前向输出列表的下标对应。
计算所有链接权重的梯度,更新链接权重
目前我们有了:
- 每个神经元的输出
- 每个神经元的输出误差
- 每个神经元的各个前驱神经元的输出
根据梯度公式,可以快速求出汇入到神经元的每条链接的梯度:
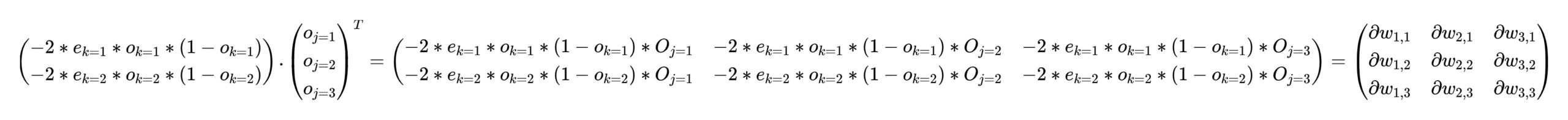
计算仍旧是逐层完成的,因为涉及到多个权重矩阵。
|
1 2 3 4 5 6 7 8 9 10 11 |
""" 梯度下降(链接权重) """ for i in range(len(self.layer_weights)): if i != len(self.layer_weights)-1 or self.output_activation: gradients = np.dot(-2*layer_errors[i]*layer_outputs[i+1]*(1-layer_outputs[i+1]), layer_outputs[i].T) else: # 经验B:如果输出层没用激活函数,那么这层链接的梯度有差别 gradients = np.dot(-2*layer_errors[i], layer_outputs[i].T) # 经验C:求出的是一批样本的梯度和,取平均梯度用作更新 self.layer_weights[i] -= self.learning_rate * (gradients / len(inputs)) |
每一颗神经元的输出与误差做简单代数乘法,然后再通过矩阵点乘与前一层每个神经元输出做乘法,可以直接得到相关链接的梯度。
这里第1个注意点,就是如果输出层不应用激活函数的话,那么最后1个隐层与输出层之间的梯度公式推导出来是不一样的,这就是上面if逻辑要解决的问题,如果忽视这个点就会导致回归问题始终无法收敛。
这里第2个注意点更加特殊,我们知道输入进来的x,y可能是batch的,也就是一次性给进来N个样本。
此时N个样本经过一轮前向传播之后,每个神经元上的输出也是N个,分别对应N个样本;经过反向传播后,每一个神经元的误差也是N个,分别对应N个样本各自的误差;我们按上述梯度公式计算的话,实际得到每条链接的梯度是所有样本梯度的和,因此需要除以样本个数得到这个batch为链接带来的平均梯度。(大家可以在纸上写一下输入N个样本的时候,每个神经元的output和error矩阵,就明白为什么上述梯度公式中的点乘计算的是所有样本的梯度平均了,很容易理解)
因为目标函数是损失最小化问题,所以就减去学习率*梯度,朝着令损失更小的方向移动权重即可。
预测函数
预测就是一轮前向传播,得到输出,因此代码和训练时的前向传播代码完全一样,抄了一遍:
|
1 2 3 4 5 6 7 8 9 10 11 |
""" 预测函数 inputs:输入 """ def predict(self, inputs): x = np.array(inputs, dtype=np.float).T for i in range(len(self.layer_weights)): x = np.dot(self.layer_weights[i], x) if i != len(self.layer_weights) - 1 or self.output_activation: # 非输出层 or 输出层应用激活 x = expit(x) return x.T # 行优先返回 |
测试模型
我们造一个简单的线性回归数据集,让模型学习这个数据集,看模型能否完美的拟合:
|
1 2 3 4 5 6 7 8 9 |
import matplotlib.pyplot as plt # 线性函数 def f(x): return 5*x # 生成训练集 train_x = np.arange(0,1,0.01).reshape(-1,1) train_y = f(train_x) |
生成的train_x就是一组x,f(train_x)就是一组y,符合线性函数5x。
每次都是全量样本输入进去,训练上足够的轮数,让它每次学习一小步(学习率不高):
|
1 2 3 4 5 6 7 8 9 10 11 |
# 定义神经网络 nn = NeuralNetwork(input_size=1, hidden_layers=[5,4,2], output_size=1, learning_rate=0.001, output_activation=False) # 训练 for i in range(1000000): nn.train(train_x, train_y) # 均方误差 if i % 100000 == 0: mse = np.mean(np.power(nn.predict(train_x)-train_y, 2)) print('epoch=%d mse=%f' % (i+1, mse)) |
每次训练后,我们让模型对这批x预测y,然后计算y和目标值之间的均方误差,随着训练会发现误差越来越小:
|
1 2 3 4 5 6 7 8 9 10 |
epoch=1 mse=8.274988 epoch=100001 mse=0.034958 epoch=200001 mse=0.015758 epoch=300001 mse=0.008295 epoch=400001 mse=0.005622 epoch=500001 mse=0.004212 epoch=600001 mse=0.000981 epoch=700001 mse=0.000607 epoch=800001 mse=0.000714 epoch=900001 mse=0.000761 |
然后我们将原始x,y画成线,把模型根据x而预测的y画成另一条线,发现高度重合:
|
1 2 3 |
# 绘制图像 plt.plot(train_x, nn.predict(train_x), c='red') plt.plot(train_x, train_y, c='green') |
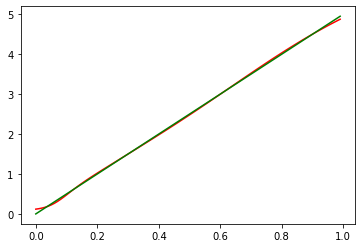
模型对于它见过的数据区间的拟合能力很不错,但是我们也注意到对于没见过的x区间之外,似乎曲线开始弯曲了,这也没得办法。
关于神经网络的理论和实现就到此结束,欢迎大家留言交流。
如果文章帮助您解决了工作难题,您可以帮我点击屏幕上的任意广告,或者赞助少量费用来支持我的持续创作,谢谢~

怎么会有人像鱼儿如此优秀
误解,我只会简单的。
1
1