numpy机器学习 – 波士顿房价回归
本文分享”波士顿房价”的数据分析与线性回归问题。
加载数据
这是关于波士顿地区的房价预测问题。
每一行代表波士顿一个郊区的各种特征,最后一列是该郊区的房价。
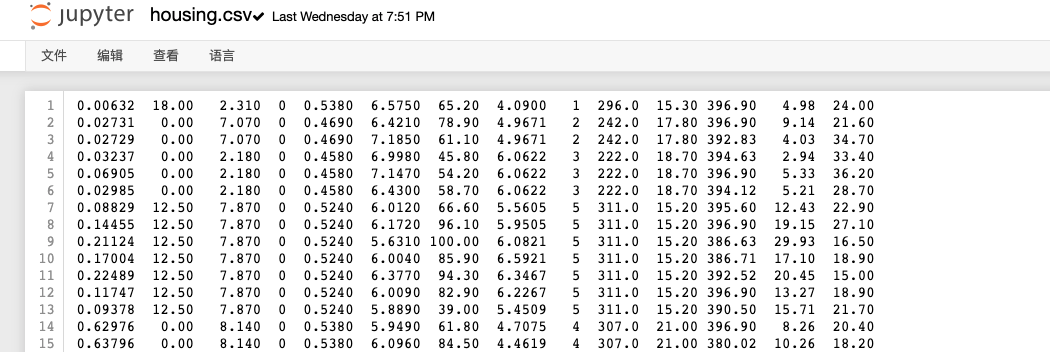
因为CSV没有表头,我们自己指定列names,用正则\s+解析字段:
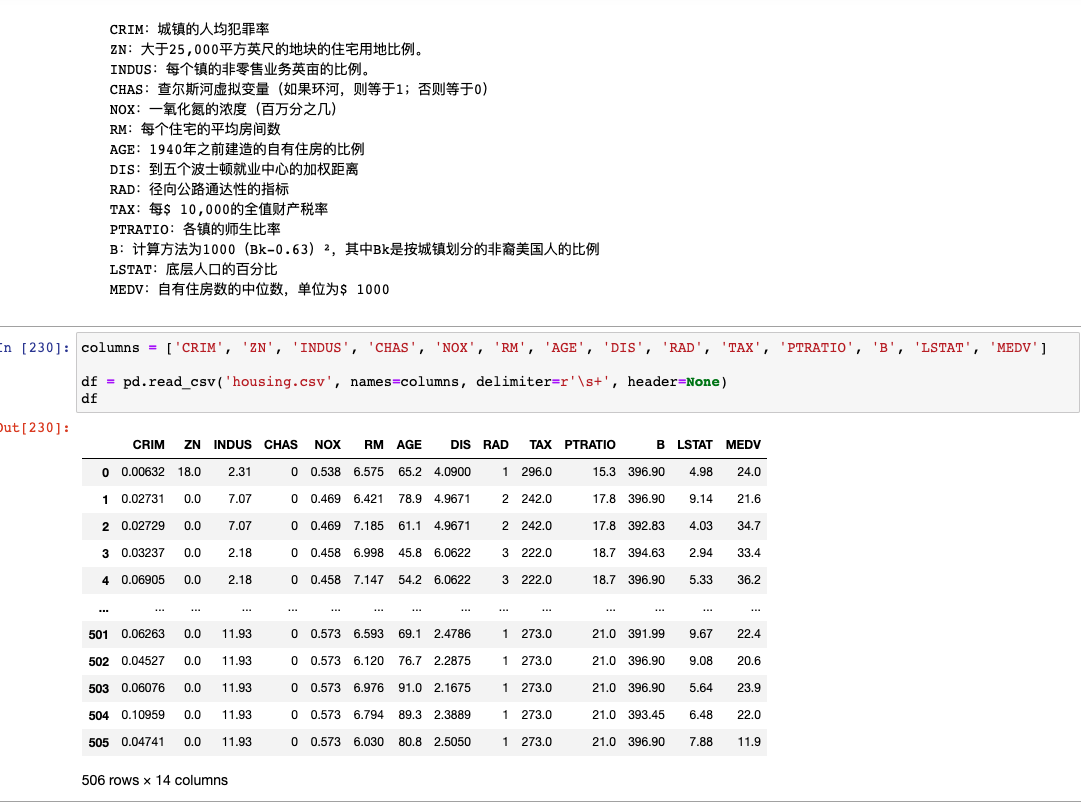
MEDV是该郊区的房价(单位是万),我们要用前面那些特征来回归预测MEDV,所以我们要分析什么特征与房价有关。
数据观察
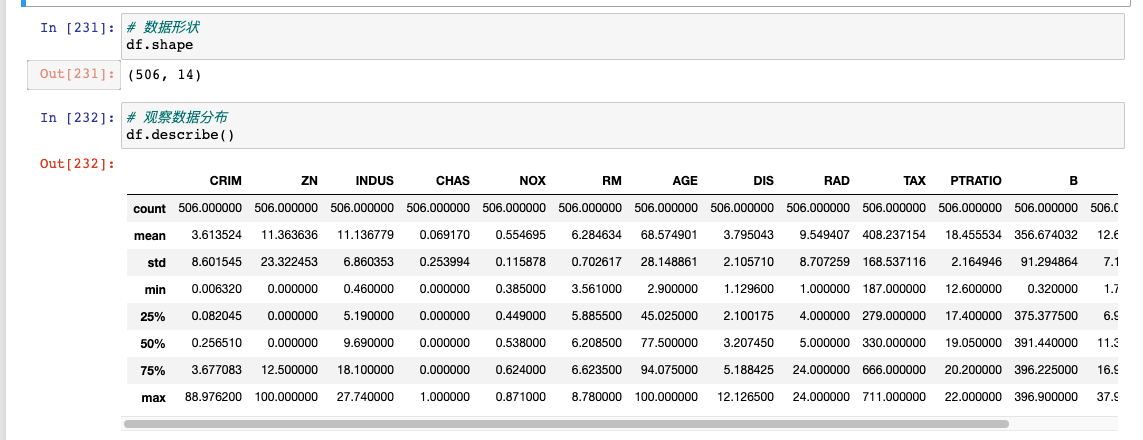
可以简单看一下各个特征的分布情况,但是这样的数据不直观,不仔细看发现不了什么信息。
各个特征的数值分布情况,用hist方法可以很方便的画出直方图:

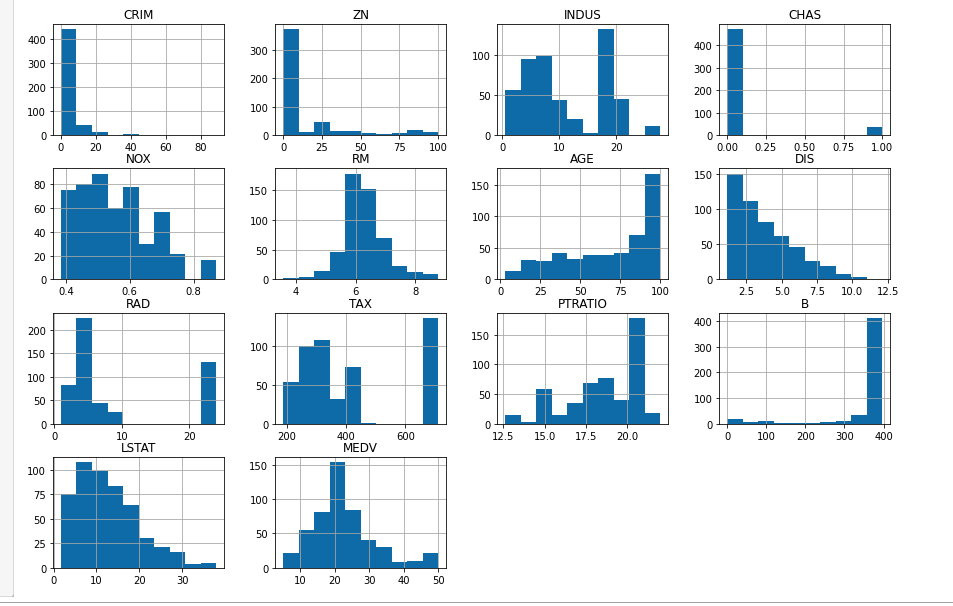
可以看看每种特征的取值范围和聚集区域,但是这种图看不出各个特征与MEDV房价之间的相关关系,实用性比较虚。
相关性分析(可视化)
我们关注的是特征和房价之间的关系,所以得看看哪些特征和房价有关系,这时候就得懂“相关性”概念。

我们有13个特征,因此绘制13张图来分别刻画它们与房价MEDV之间的关系。
绘制采用散点图,将506个样本的某个特征作为X坐标,房价作为Y坐标,绘制出它们的分布关系:
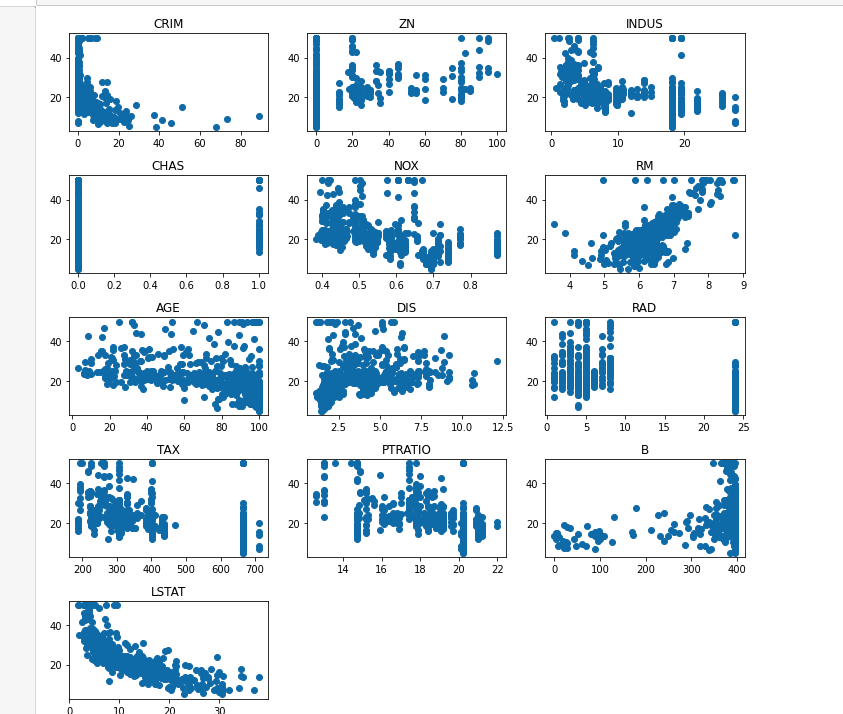
以第一张图为例,横坐标是样本的CRIM特征,纵坐标是样本的MEDV房价。
特征和房价的相关性程度可,可能是下面的某种情况:
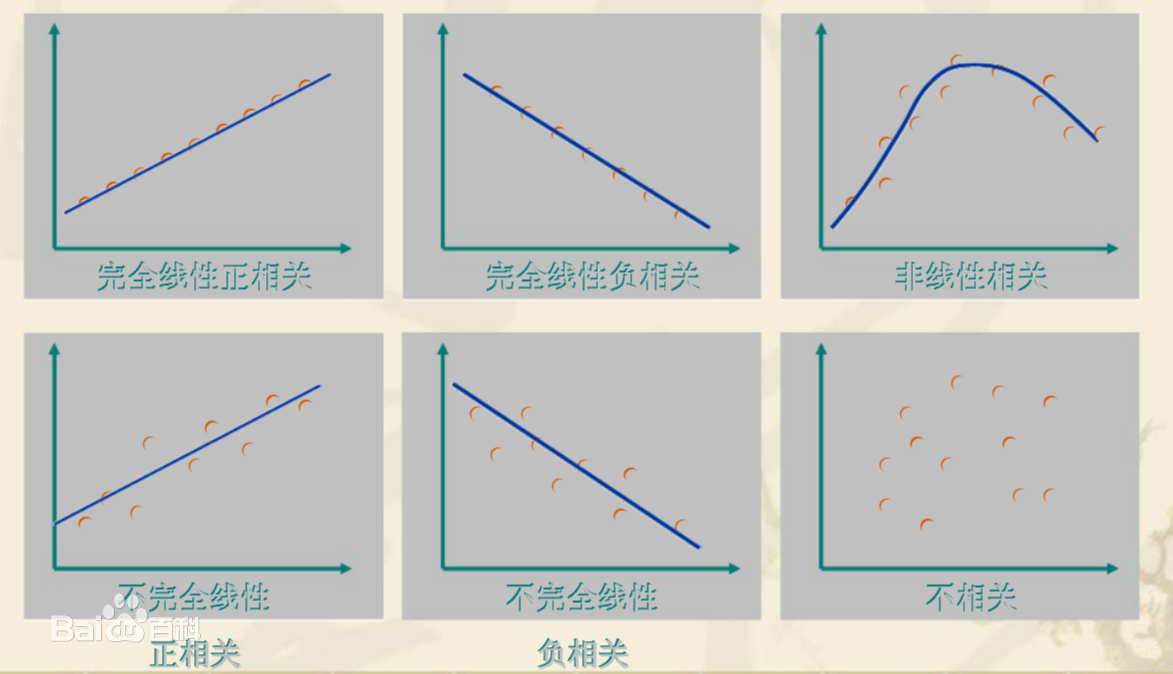
- 如果X变大Y也变大,那么就是正相关的
- 如果X变大Y变小,那么就是负相关的。
- 如果点排列成直线那就是完全线性相关性,否则就是不太完全的相关性。
- 如果点乱七八糟的分布,那么X和Y之间没有什么相关性。
我们现实情况中遇到的应该大多是”不完全线性“的相关性,可能是正相关或者负相关。
另外第1行第3张图是”非线性“相关的,也就是说函数图像可能是y=x^2这样的曲线,这种也算相关性,但它不是线性相关性而是非线性的相关性,我们用可视化的方式来发现这种数据规律,才能知道应该如何将特征用到我们的模型构建中(例如线性关系可以用一次项,非线性相关可以用2次项)。
我们通过另外一个图再来理解一下:
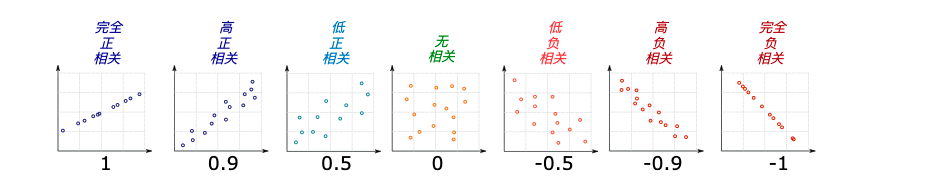
有了这样的了解,我们看看上面各个特征与房价之间的关系, 发现:
- RM与房价之间正相关
- LSTAT与房间之间负相关
- 其他的不是很强烈,所以先不考虑。
如果我们做一个回归函数长这样:
y=a+b*RM+c*LSTAT
经过对训练数据的拟合后,a,b,c系数充分学习,即可对任意(RM,LSTAT)进行房价预估,同时我们也猜得出b应该是个正数,c应该是个负数,因为它们与房价呈现正相关与负相关。
除了可视化观察之外,我们也可以求所有特征与房间之间的相关性系数,量化的观察特征与房价之间的相关性强弱:
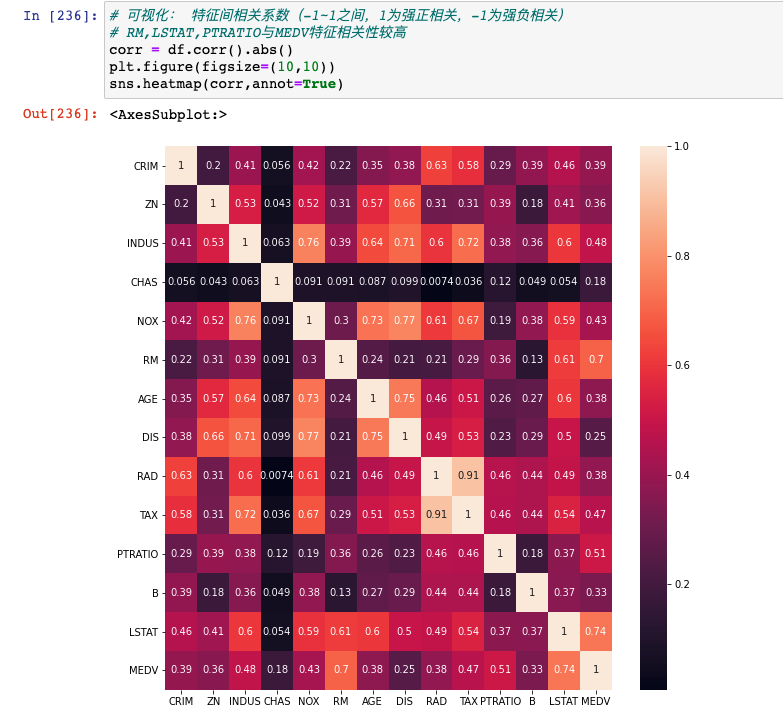
我们只关心13个特征和MEDV之间的相关性系数,可以看到RM与MEDV是0.7,LSTAT与MEDV是0.74,和之前的图片互相印证。
相关性系数的范围是-1~1,越接近1表示强正相关,越接近-1表示强负相关,越接近0表示不相关,其计算方法为:
这里x就是某个特征,y就是房价,对上述公式对样本集求解后,即可得到Rxy。
回归模型
现在我们可以基于RM和LSTAT训练房价回归模型了,根据之前的几篇博客我们不用任何库,直接纸上推导好梯度下降公式后直接训练系数项即可:

训练时需要对RM和LSTAT特征进行标准化,否则计算出的梯度会太大,如果学习率不够小的话会导致theta在目标函数的谷底左右跳跃,无法达到最低位置,也就是我们常说的无法收敛:

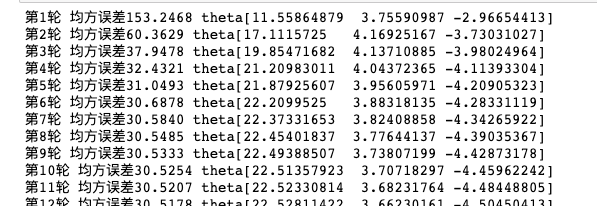
训练过程中,我们不停的梯度下降系数项,然后打印每一轮的均方误差会发现它不停的变小并趋于稳定,说明此时梯度已经消失(接近0),目标函数在当前theta位置已达谷底:
为了证明训练好的回归模型准不准,我们可以顺序的将所有样本点的真实房价和预测房价都画出来,看一下曲线的吻合度:
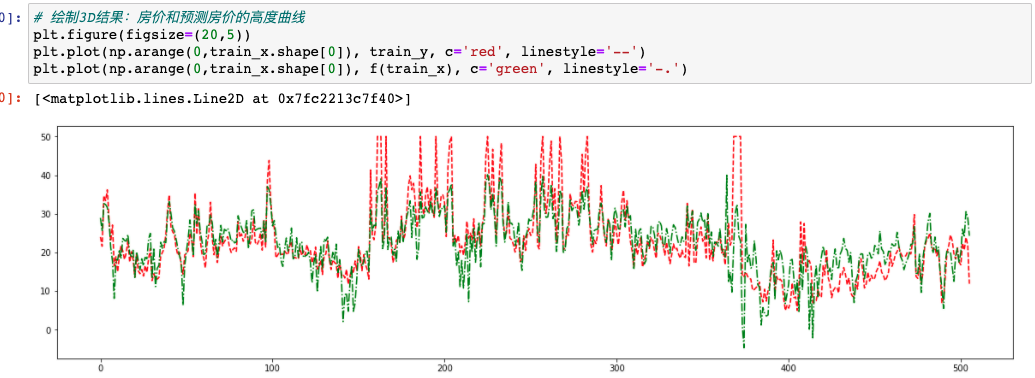
为什么要这样来看效果呢?因为这个模型是2个特征与房价之间的关系,也就是说3个变量(都是连续值)在平面上是无法绘制出图像的,因此只能说看一下预测值和实际值之间的差异程度,并不能将特征本身刻画到图像上了。
相关资料
”相关性分析“还有一些重要的认知,建议大家看一下数学乐的描述:https://www.shuxuele.com/data/correlation.html。
我在B站录制了视频版本,如果大家对文字版有理解困难可以看一下:https://www.bilibili.com/video/BV1sK411c71P/。
如果文章帮助您解决了工作难题,您可以帮我点击屏幕上的任意广告,或者赞助少量费用来支持我的持续创作,谢谢~


1
1
1
Great post on using NumPy for machine learning! The example of predicting housing prices with a simple linear regression model is very insightful and easy to follow. For those interested in more unique applications of predictive modeling, such as customer preferences, you might find interesting correlations when looking at niche markets like the male sex dolls industry. Keep up the excellent work!