本文分享如何证明与实现一个神经网络，本篇博客拖延了很久，因为要深入浅出的讲明白是需要花点功夫的（画神经网络图、用latex推导公式）。

理论简述

神经网络看似复杂，实际数学知识非常简单。

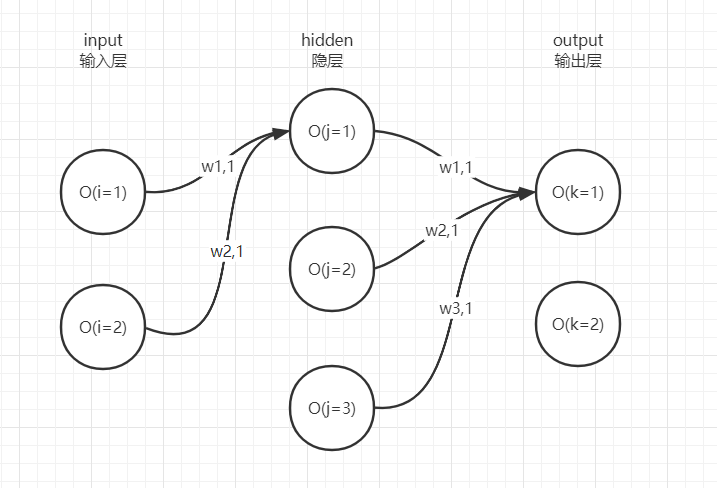
神经网络的关键是搞懂3个东西：

• 神经元的输入？
• 神经元的输出？
• 神经元之间的链接？

前向传播

从上图看，input层的2个神经元到hidden层第1个神经元分别有1条链接，因此input两个神经元的输出经过链接上的权重加权求和后，就是hidden第1个神经元的输入，那么hidden第1个神经元的输出是多少呢？

我们首先搞懂input神经元的输出是什么再继续，这里O(i=1)与O(i=2)就是2个input神经元的输出，其实就是（训练样本/预测样本的）原始特征，不需要做任何变换。

来到hidden层，实际上hidden第1个神经元的输出O(j=1)是对其输入的加权求和结果O(i=1)*w1,1 + O(i=2)*w2,1执行一次激活函数得到的，激活函数可以是我们比较熟悉的sigmoid。

这里就可以提出第1个神经网络的矩阵运算公式：前向传播。

利用矩阵点乘，我们可以轻松利用input层的输出矩阵与链接权重矩阵快速计算出hidden层所有神经元的输出：

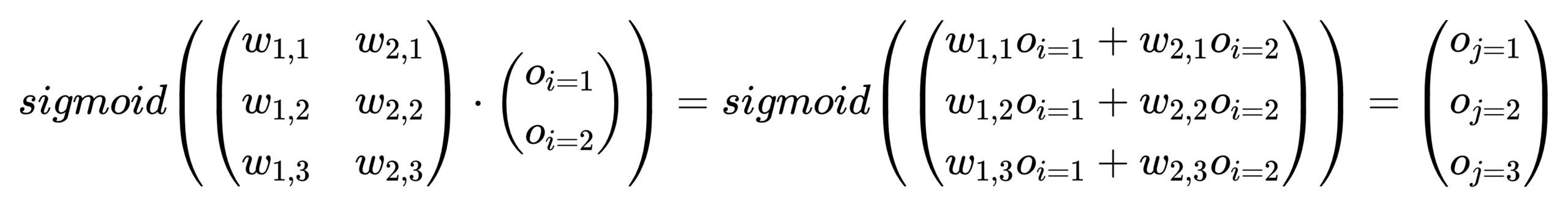
通过矩阵运算可以直接求出hidden层所有神经元的输入，最终统一做sigmoid即可得到hidden层神经元的输出。

因此，我们只要根据网络结构，为层与层之间初始化尺寸正确的随机w链接矩阵，即可逐层执行矩阵乘法快速求出output层神经元的输出了。

（注：如果是类似房价预测的回归问题，output层的输出不需要应用激活函数，因为激活函数的性质都是会限制y在某个很小的范围内，例如sigmoid的y值是介于0~1之间的）

我们需要记住每一层每一个神经元的输出，因为后续训练需要用到它们，这里先提一句。

反向传播误差

神经网络训练其实就是调整每一层之间的链接权重，最终达到拟合目标的效果。

input经过前向传播到达output层产生输出，我们需要求出和目标值之间的误差。

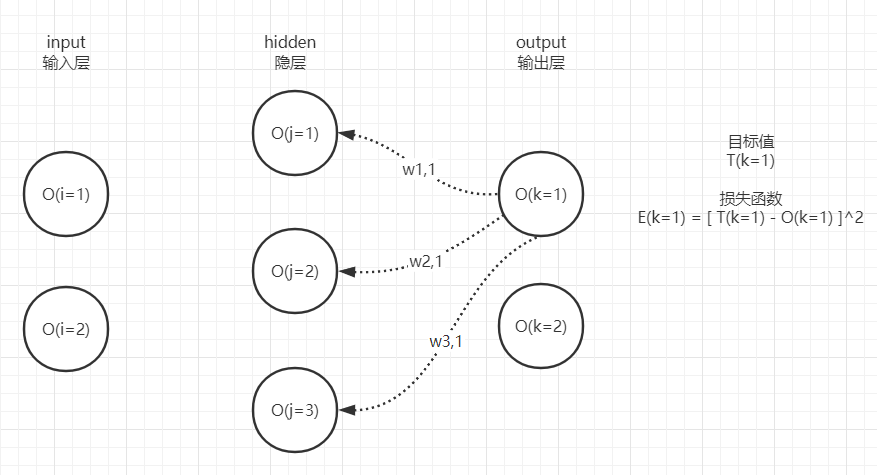
output可能有1个至多个神经元，这取决于模型的任务是什么，实际上每个神经元都有自己的误差，因此实际情况如下图：

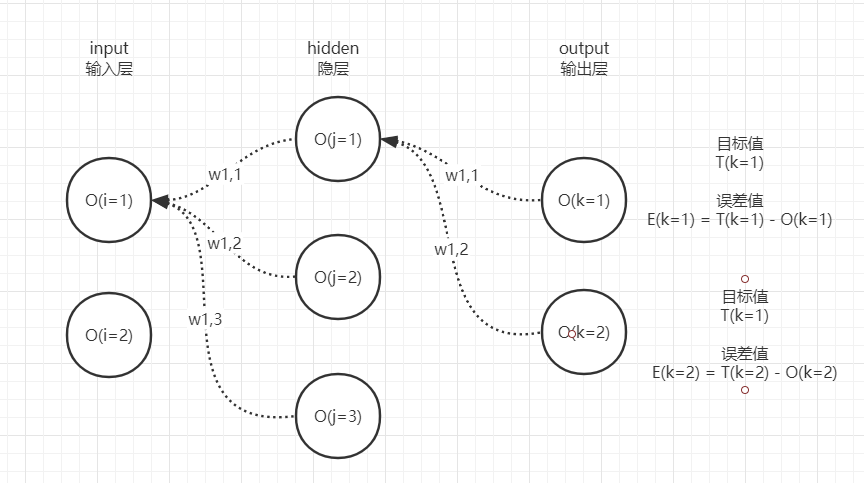
T(k=1)和T(k=2)分别表示2个output神经元的正确目标值，分别与各自的O(k)做减法即可得到output神经元的2个误差值E(k=1)和E(k=2)。

在谈论应该如何调整链接权重才可以令“当前预测的误差更小”这个终极模型训练问题之前，我们需要先做一件重要的前置工作：

让output层神经元的误差反向传播到hidden层的每一个神经元，只有hidden层神经元身上有了误差，我们才能有办法优化input层和hidden层之间的链接权重。

如果不反向传播误差到hidden神经元身上，我们只能依靠output层的误差训练hidden与output之间的链接权重，这个从图像上很容易理解。

从直觉来说，hidden层第1个神经元的误差只能沿着w1,1和w1,2两条链接来反向传播，因此hidden第1个神经元的误差E(j=1)变成了加权求和问题：

E(j=1) = E(k=1)*w1,1+E(k=2)*w1,2

根据图片理解，前向传播时hidden第1个神经元同时会向output的2个神经元传递信号，因此output层2个神经元的误差应该也要反向归因于hidden层第1个神经元，同时遵循哪条链接权重小则连带的误差越小，符合直觉。

同理，当我们求出了hidden层3个神经元的误差后，就可以继续反向传播误差到input层，但实际上我们不需要继续这样做，根本原因是input和hidden之间的链接权重训练只依赖于hidden层的误差，下面推导梯度公式时就会明白。

如果你看着图片仔细想象一下神经元之间的信号沿着链接流动的话，你就不难看出反向传播正如其名，如果说前向传播是从左往右的逐层计算，那么反向传播就是从右往左的逐层计算，即为了计算每一层神经元的输出误差，这是很巧妙的设计。

借助矩阵点乘，反向传播也仅仅是逐层的矩阵运算而已，可以非常快的求出每一层每一个神经元的误差，我们以上图output->hidden传播误差为例：

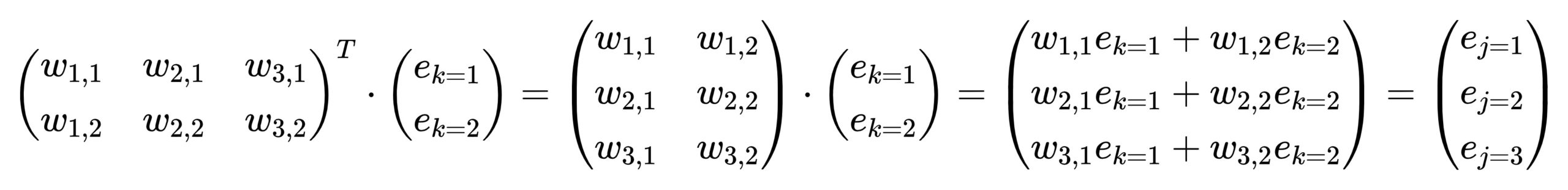
我们只需要将hidden->output的权重矩阵转置，然后与output层的误差矩阵做点乘，即可直接求出hidden层每个神经元的误差。

经过反向传播，除了input层外，我们应该记住每一层每一个神经元的误差，这是我们训练链接权重的前提，后续求梯度的时候会印证这一点。

梯度下降

以output层误差为例，为了让2个神经元的误差E更小，我们需要定义损失函数：

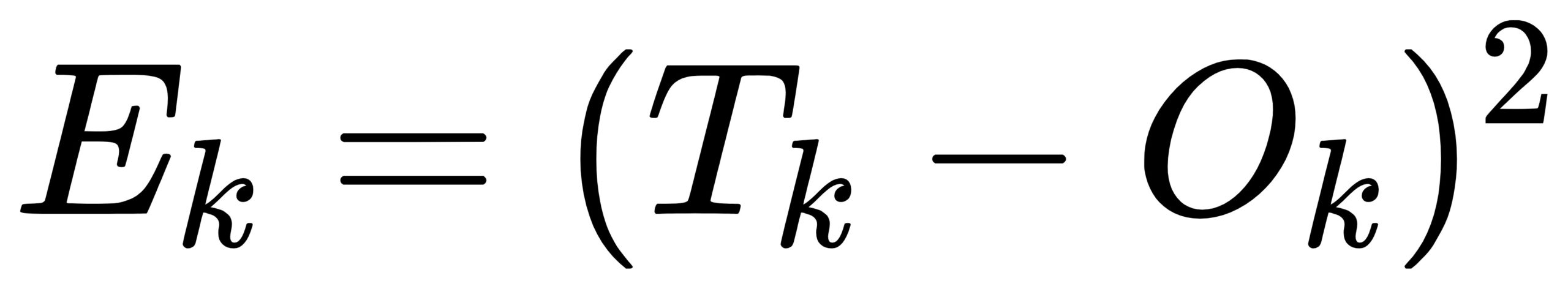
但是必须注意，这里的k指output层某个神经元，而不是指output层的所有神经元，比如k=1则意味着Ek是output层第1个神经元的损失函数，为了让这个损失更小，我们能够调整的是仅仅是与之相连的链接权重：

可见：

• 对于k=1的神经元，其损失函数E(k=1)只能调整与之链接的w11、w21、w31；
• 对于k=2的神经元，其损失函数E(k=2)只能调整与之链接的w12、w22、w32；

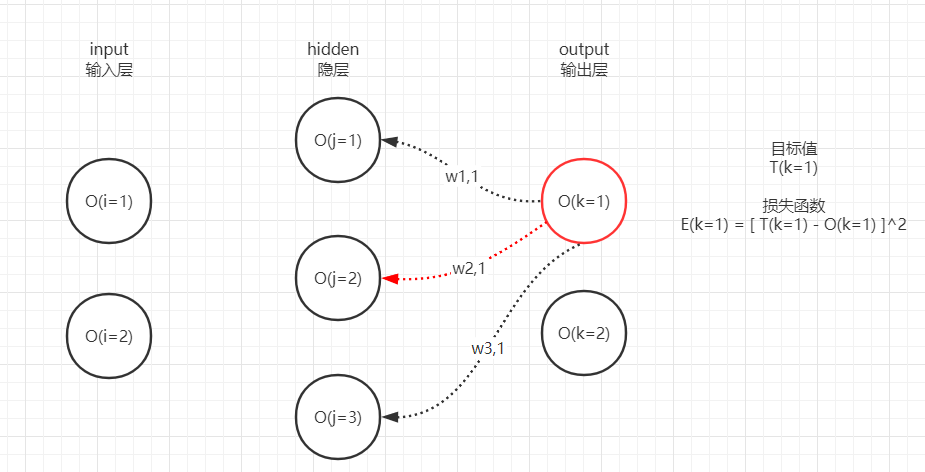
因此，我们只要分析出E(k=1)是如何对w11、w21、w31链接权重进行梯度下降的，即可同理梯度下降k=2上的链接权重w12、w22、w32，所以我们再次回到这张图：

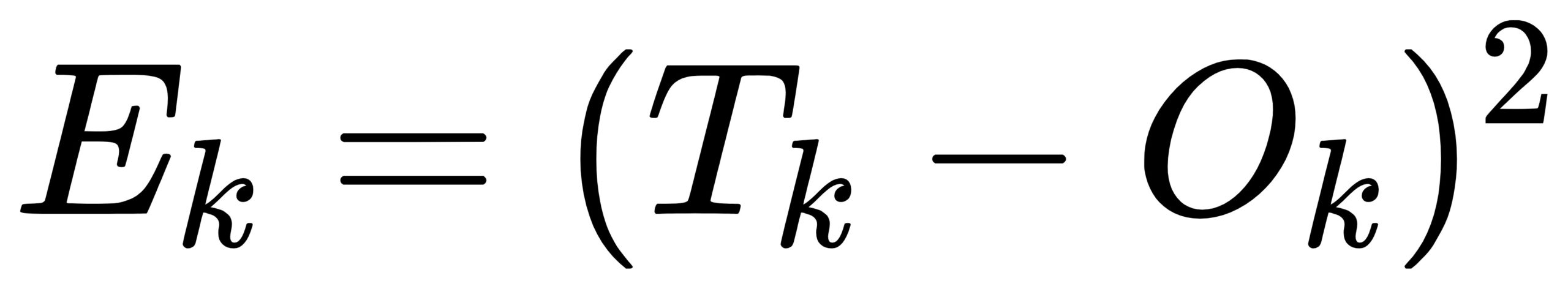
其中Ok是第k个output神经元的输出，是关于hidden层神经元经过与一组w链接权重的加权求和再执行激活函数（以sigmoid为例）得到的。

因此，Ek函数最小化就是找到Wj,k的修正方向，也就是求Wj,k的梯度：

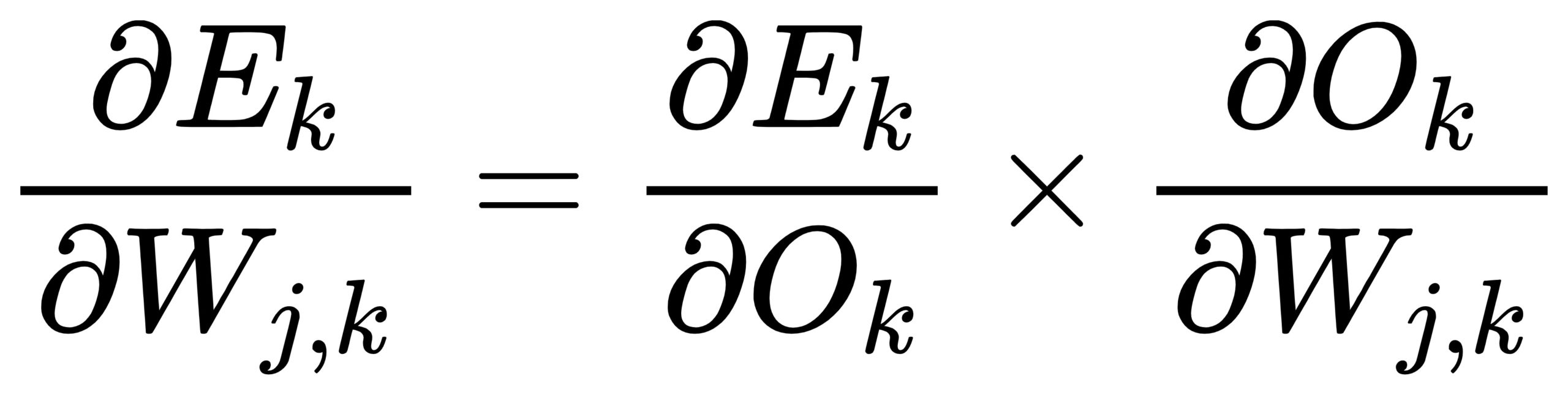
这里要注意，假定当前要优化的k=1节点的误差，那么我们能够优化的链接wj,k中的k就是1，j可以是1、2、3，我们推导上述公式时必须假定当前推导的是某一条链接的权重梯度，即只求该权重的偏导数：

同时，因为Ok是关于Wi,j的函数，所以上述偏导公式需要通过复合函数变换得到。

上述第1部分很容易求解，只需要将Ok视为变量：

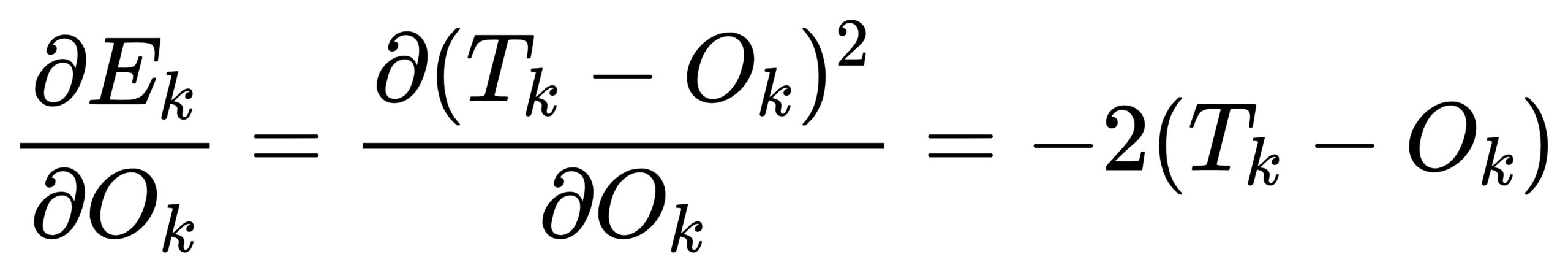
第2部分我们首先需要写出Ok函数（仍旧是上图中红色部分），其实Ok就是前向传播时从hidden层加权求和激活后得到的：

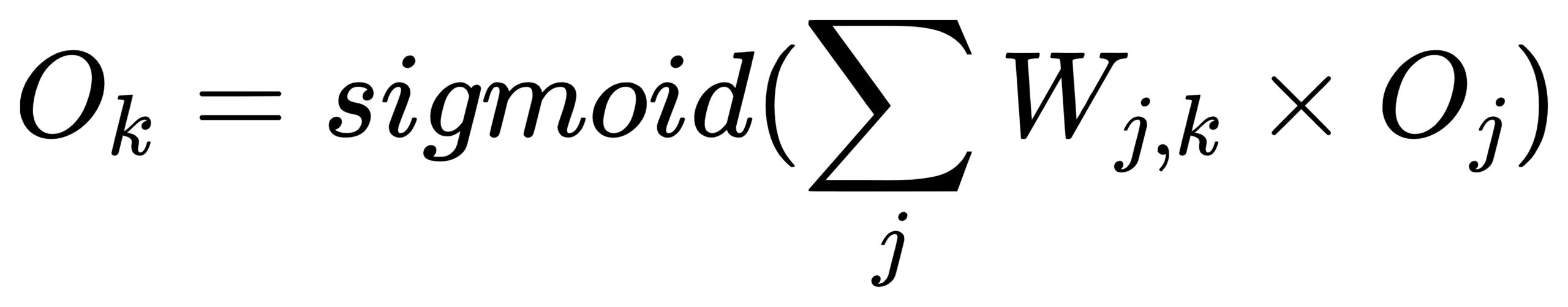
对上图红色Ok求红色链接Wj,k的偏导，会发现再次呈现复合函数，因此做变换：

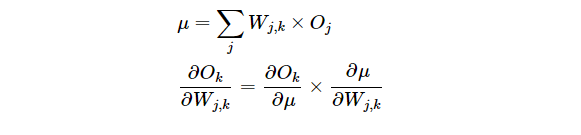
两项求导结果是显而易见的：

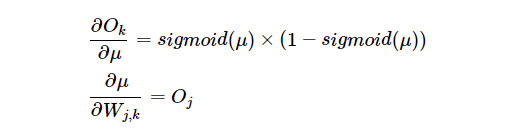
将上述2项乘起来，再和最上面Ek关于Ok的偏导相乘，最终公式为：

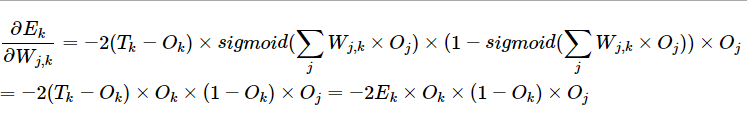
你会发现将μ带入最终结果后，sigmoid项正好是Ok，最终该条链接权重的梯度公式是关于：

• 链接右侧神经元的误差
• 链接右侧神经元的输出
• 链接左侧神经元的输出

运算得到的结果即该链接的梯度，最终只需要对Wj,k减去这个梯度*学习率即可完成该链接权重的梯度下降。

回到图中再次说明，即我们的目标是优化红色的链接权重，则计算时需要用到：

• 绿色神经元的输出和误差
• 蓝色神经元的输出

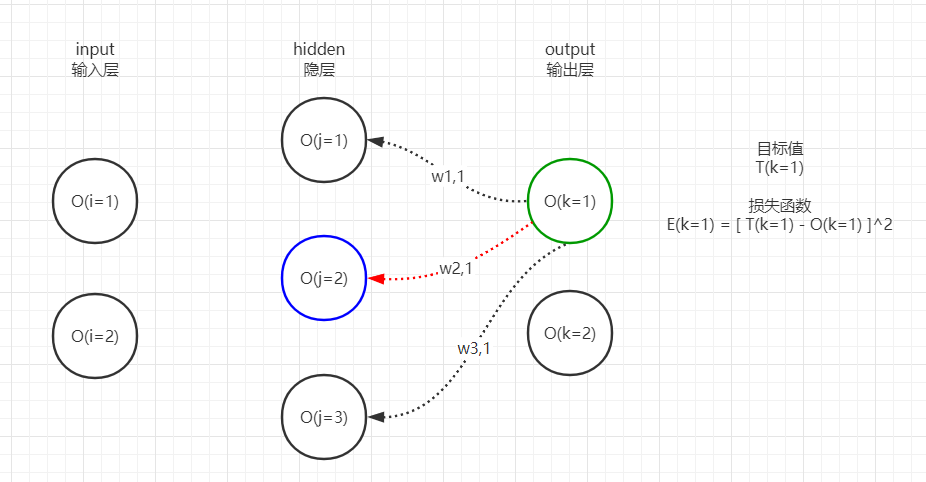
而这些在我们前向传播和反向传播误差时，均已记录了下来。

如果你仔细在脑海中想象画面的话，要一次性求出hidden层与output层之间每条链接权重的梯度，只需要像下面这样的一个矩阵运算即可得到每条链接的梯度（点击图片放大看）：

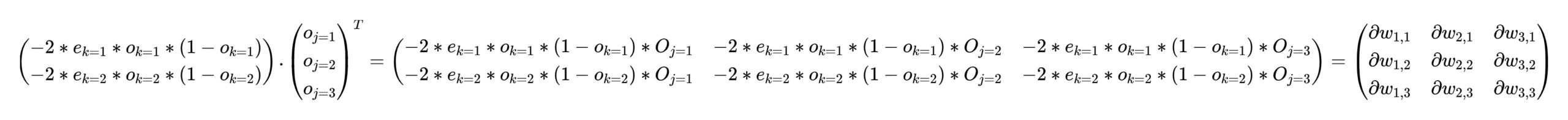
注意Ok与Ek是output层每个神经元上的普通乘法就可以得到。

然后完成梯度下降就只需要做一次矩阵减法：

至此hidden与output层之间的所有链接权重均朝着各自能够令Ek更小的方向移动完成。

至于input和hidden层之间的链接则遵循同样的公式：

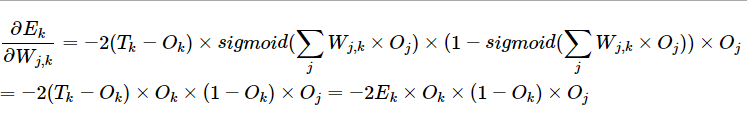
Ek、Ok、Oj换成对应的input与hidden之间的对应矩阵即可，无需进一步证明，这就是为什么前向传播时需要保留每一层每一个神经元的输出O，以及反向传播误差时需要记录每一层每一个神经元的误差E的原因，即梯度下降公式依赖于它们。

结束语

关于神经网络的理论部分就到这里，有任何问题欢迎留言。

代码我放在了这里：https://github.com/owenliang/MLP，我会在后续的博客中简单讲解一下实现过程中要注意的问题，相信理解原理的你现在也应该大致能去尝试自己写一下了。

我在B站录制了视频版本，目前更新到了“前向传播”部分，对文字版理解困难的同学建议看视频：

1. 讲给小白的神经网络（第1期-前向传播）